
Hello Stardust! Today we’ll see mathematical reason behind exploding and vanishing gradient problem but first let’s understand the problem in a nutshell.
“Usually, when we train a Deep model using through backprop using Gradient Descent, we calculate the gradient of the output w.r.t to weight matrices and then subtract it from respective weight matrices to make its(matrix’s) values more accurate to give correct output”
But what if the gradient becomes negligible?
When the gradient becomes negligible, subtracting it from original matrix doesn’t makes any sense and hence the model stops learning. This problem is called as Vanishing Gradient Problem.
We’ll first visualise the problem practically in our mind. We’ll train a Deep Learning Model with MNIST(you know this) dataset with 1,2,4 and 5 hidden layers and see the effect of using different architecture on the output(accuracy doesn’t increase always! ?).
You can access to the complete code here. For this article I’m just using snapshots of the code. I have used Deep Learning Studio’s Jupyter lab to execute the code. If you’re unaware of this awesome Deep Learning Tool, check out my article on that.
Iris genus classification|DeepCognition| Azure ML studio
Model with 1 hidden layer.
line 1: 784 denotes the input neurons,30 denotes neurons in hidden layer 1, 10 denotes number of outputs.

Here the term ‘Length of weight matrix of ‘ith’ hidden layer’ is the magnitude of the weight matrix of first hidden layer. It can be considered as the speed with which a particular hidden layer learns features(roughly).
We’ll use this term to compare the speed of different hidden layers of different models.
Speed of First hidden layer in first model:0.103165(remember this!)
Model with 3 hidden layers:
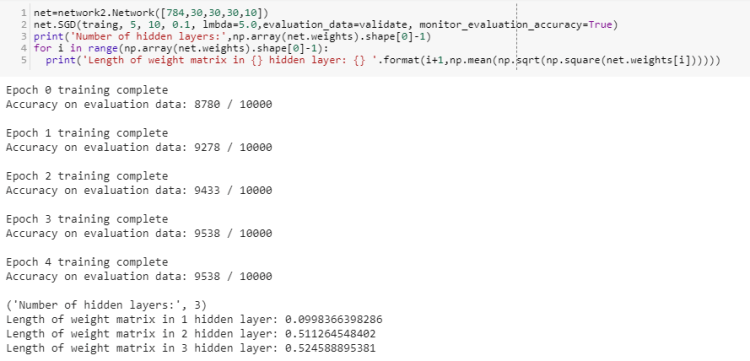
Observations:
- Learning speed of first hidden layer:0.09983(less than speed of previous model’s 1st hidden layer).
- Learning speed of ith layer is generally more than (i+1)th layer.
Let’s move on to MNIST with 4 and 5 layers
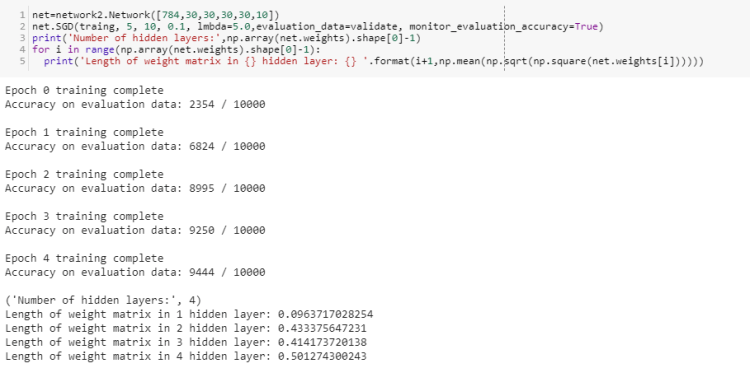
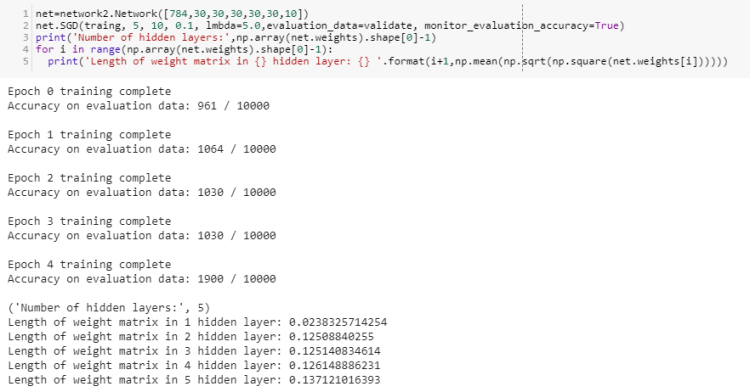
Learning speed of ith hidden layer keeps on decreasing as we have more deeper models i.e a model with more hidden layers.
Trending AI Articles:
1. Natural Language Generation:
The Commercial State of the Art in 2020
4. Becoming a Data Scientist, Data Analyst, Financial Analyst and Research Analyst
In 5 hidden layers we even lose the accuracy of the model.
The Mathematical Reason.
Consider a neural network with 4 hidden layers with a single neuron in each matrix.
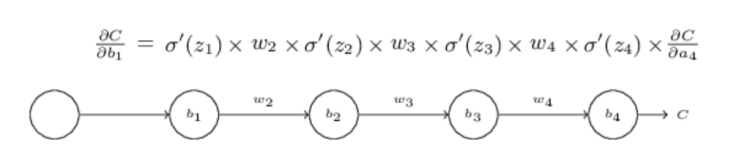
The computation graph for the neural network above is:

In forward propagation, we just multiply the input with weight matrices and add bias as shown above. We then find the sigmoid of the output.

During backprop, we find the derivative of the output w.r.t. different weight matrices in order to make our output more accurate. Suppose that we want to find derivative of C(output) w.r.t weight matrix (b1).
The terms which are going to be included in this are:

The sigmoid’(z1),sigmoid’(z2).. etc are less than 1/4. Because derivative of sigmoid function is less than 1/4. See below. The weight matrices w1,w2,w3,w4 are initialized using gaussian method to have a mean of 0 and standard deviation of 1. Hence ||w(i)|| is less than 1. Therefore, in derivative we multiply such terms which are less than 1 and 1/4. Hence on multiplying such small terms for a huge number of times we get very small gradient which makes the model to almost stop learning.
The reason that if we have deeper models than starting hidden layers will have low speed of learning is: we move deeper as we reach the starting hidden layers during backprop and hence more such terms are involved which makes the gradient small.
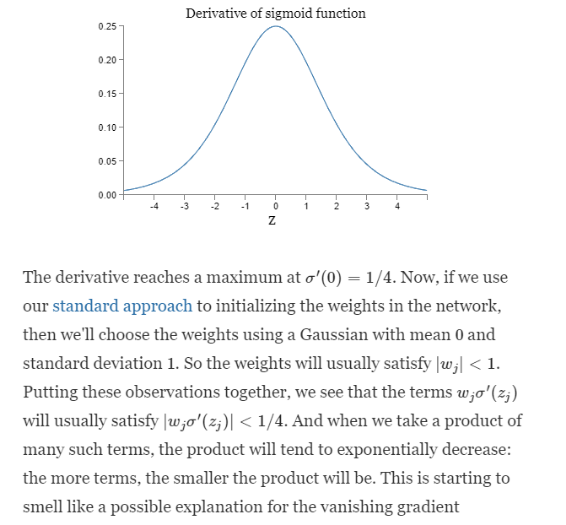
Similar is the case with exploding gradient, If we initialize our weight matrices with very large values, then the derivative will be very large and hence the model will have highly unstable training.
Thanks for Reading..guys.
Don’t forget to give us your ? !




Exploding And Vanishing Gradient Problem: Math Behind The Truth was originally published in Becoming Human: Artificial Intelligence Magazine on Medium, where people are continuing the conversation by highlighting and responding to this story.
