Gradient Descent Explained

Gradient descent is an optimization algorithm used to minimize some function by iteratively moving in the direction of steepest descent as defined by the negative of the gradient.

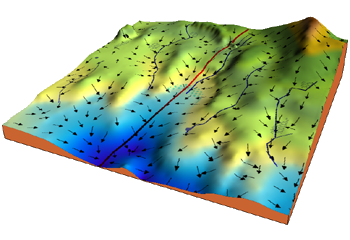
Consider the 3-dimensional graph above. Our goal is to move from the top right corner of the mountain, which can be described as a high cost, to a dark blue sea below it, which can be viewed as a low cost. The arrows represent the steepest descent from any given point that decreases the cost function as quickly as possible.

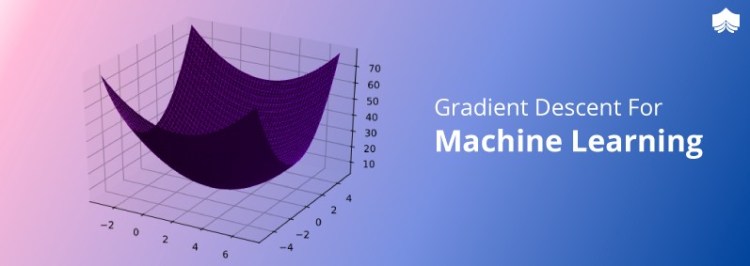
Starting at the top of the mountain, we will take baby steps downhill in the direction where the gradient is negative. After that, we recalculate the negative gradient and take another step in a specified direction. We continue this process until we get to the bottom or local minimum.

Learning Rate

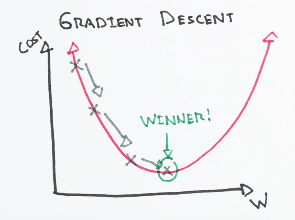
The size of each step is called a learning rate. If you have a high learning rate it means your descent will be much faster, but you will risk overshooting the local minima. With a slow learning rate, however, it will be much more precise, but it will be time-consuming. Finding the “right” learning rate is very important.

Cost Function

The loss function describes how well the model will perform given the current set of parameters (weights and biases), and gradient descent is used to find the best set of parameters. ( Clare Liu)

Top 4 Most Popular Ai Articles:

1. Natural Language Generation:
The Commercial State of the Art in 2020

2. This Entire Article Was Written by Open AI’s GPT2

3. Learning To Classify Images Without Labels

4. Becoming a Data Scientist, Data Analyst, Financial Analyst and Research Analyst

Math
Cost Function
?(?,?)=1?∑?=1?(??−(???+?))2

Gradient Descent

?′(?,?)=[????????]=[1?∑−2??(??−(???+?))1?∑−2(??−(???+?))]

Code

def update_weights(m, b, X, Y, learning_rate):
    m_deriv = 0
    b_deriv = 0
    N = len(X)
    for i in range(N):
        # Calculate partial derivatives
        # -2x(y - (mx + b))
        m_deriv += -2*X[i] * (Y[i] - (m*X[i] + b))

        # -2(y - (mx + b))
        b_deriv += -2*(Y[i] - (m*X[i] + b))

    # We subtract because the derivatives point in direction of steepest ascent
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate

    return m, b

References:

• Gradient Descent – ML Glossary documentation
• 5 Concepts You Should Know About Gradient Descent and Cost Function – KDnuggets
• Machine Learning: What is Gradient Descent?

Don’t forget to give us your ? !

---

Gradient Descent Explained was originally published in Becoming Human: Artificial Intelligence Magazine on Medium, where people are continuing the conversation by highlighting and responding to this story.

Via https://becominghuman.ai/gradient-descent-explained-1d95436896af?source=rss—-5e5bef33608a—4