Reinforcement Learning (RL) provides a mathematical formalism for learning-based control. In Deep Reinforcement Learning (DRL), a neural network with reinforcement learning is used to enhance the algorithm the ability to control the system with extremely high-dimensional input spaces such as images [1]. Learning from limited samples is one of the challenges which can be faced when DRL is applied to a real-world System. Almost all real-world systems are either slow, fragile, or expensive enough that the data they produce is costly, and policy learning must be data-efficient [2]. Model-based reinforcement learning approaches make it possible to solve complex tasks given just a few training samples.
In model-based RL, the data is used to build a model of the environment. Since the model is trained on every transition, model-based RL algorithms effectively receive more supervision, and the other benefit of those methods that they are trained with supervised learning, which is more stable opposing to bootstrapping. There are many recipes for model-based reinforcement learning [3]. The one described in the article uses the learned model as a simulator to generate “synthetic” data to augment the data set available to improve the policy. One of the problems that can arise is that policy optimization tends to exploit regions where the model is inaccurate (e.g., due to a lack of data). This issue is called model bias. Standard countermeasures from the supervised learning literature, such as regularization or cross-validation, are not sufficient to solve this issue [7]. There are two distinct classes of uncertainty: aleatoric (inherent system stochasticity) and epistemic (due to limited data). One way to deal with the exploitation of model inaccuracies is to incorporate uncertainty into the predictions of our model.
There are many possibilities to capture model uncertainty for model-based RL. Gaussian processes [5] and Bayesian neuronal networks incorporate uncertainty directly but are not suitable for complex tasks. Other Methods can be used to approximate model uncertainty like model ensembles [7] and dropout [6].
The assessment of uncertainty is not only of crucial importance in model-based RL but also in modern decision-making systems. Kahn used uncertainty estimation for obstacle avoidance and reward planning. Berkenkamp used the uncertainty estimation to make exploration safer.
Model-Ensemble
The focus of this article will be on the ensembles method. Or more precisely: How we can use an ensemble of networks to represent the uncertainty and apply it to reinforcement learning algorithms. Beginning with some results from our experiment, where we trained an ensemble of 3 models to approximate the motion of a robot arm moving to push an object. The following diagram shows the result for the 70-steps prediction

Model-Ensemble Trust-Region Policy Optimization (ME-TRPO)
Kurutach et al. [7] propose to regularize the policy updates using an ensemble of models that can be used to model the uncertainty, to tackle the model bias problem.
In the models’ update step, a set of K dynamics models is trained with supervised learning using the data collected from the real-world. The models’ weights are initialized independently and trained on mini-batches in different orders. In the policy update step, Trust Region Policy Optimization (TRPO) [9] is used to optimize the policy using virtual stochastic rollouts. Each virtual step is uniformly sampled from the ensemble predictions, which leads to more stable learning because the policy does not overfit to any single model. The last step is the policy validation step, where the policy is validated after every n gradient updates using the K learned models. If the ratio of models in which the policy improves exceeds a specified threshold, the current iteration continues. If not, then the current iteration is terminated, and the actual policy will be used to collect more real-world data to improve the model ensemble.
Trending AI Articles:
1. Fundamentals of AI, ML and Deep Learning for Product Managers
3. Graph Neural Network for 3D Object Detection in a Point Cloud
4. Know the biggest Notable difference between AI vs. Machine Learning
The learned policy will be robust against various scenarios it may encounter in the real world.
To Evaluate the algorithm first, they compared ME-TRPO with the Vanilla Model-Based RL algorithm, to show the effect of using model-free algorithms to update the policy. They found that ME-TRPO leads to much better performance. Second, they compare it with state-of-the-art Model-Free methods in terms of sample complexity and final performance. Finally, they evaluated the used ensemble. They found that more models in the ensemble lead to improve the policy because the learning is better regularized. On the other hand, the resulted policy is more conservative because it has to get a good performance on all the models.

Model-Based Meta Policy-Optimization (MB-MPO)
Model-Based Meta Policy-Optimization [8] shares the same trajectory sampling scheme as ME-TRPO but utilizes the model-generated data differently.
In MB-MPO, meta-learning aims to learn a policy that adapts fast to new tasks. Each task corresponds to a different belief of what the real environment dynamics might be. In other words, it is the dynamics of different learned models, but they share the same action-space, state-space, and reward function.
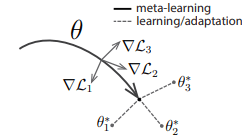
In an adaptation step, Vanilla Policy Gradient (VPG) is used to form a task-specific policy from a meta-policy

with Jk(θ) being the expected return under the policy πθ. Trust Region Policy Optimization (TRPO) is used for maximizing the meta-objective
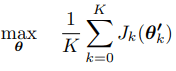
where K is the number of tasks or the number of models in the ensemble. The meta-objective aims to find a good meta-policy that can be adjusted with a gradient step to use it for K tasks and get maximum reward for each of these tasks.
Models’ update step
Trajectories are sampled from the real environment with the adapted tasks’ policies θ1,…, θK, and added to a data set D. These trajectories are used to train all models. The objective of learning each model is to minimize the L2 one-step prediction loss:
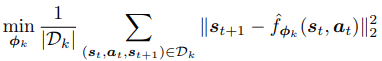
Task policies and meta-policy update step
The following pseudo-code shows that the update of the policy step uses only imaginary trajectories generated from all the models in the ensemble
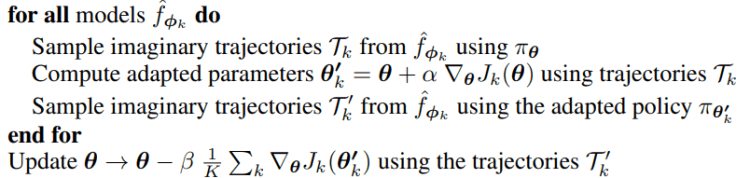
There are many advantages to this algorithm:
- Regularization effect during training this effect prevents the policy from learning sub-optimal behaviors that arise in robust policy optimization (ME-TRPO).
- Tailored data collection for fast model improvement Using K policies to collect real-world data generates diverse data. This effect accelerates correcting the imprecision of the Ensemble models leading to more rapid improvement.
- Fine-tuning the policy with VPG on the real environment leads to faster convergence than training the policy from scratch.
- Simplicity.
Model-Based Value Expansion (MVE)
The goal of Model-Based Value Expansion [11] is to improve both sample efficiency and performance by utilizing a learned dynamics model to enhance state-action value estimates, namely, to improve the targets for temporal difference learning.
For this, the authors expand the state-action value at an arbitrary state Q(s0) into an H-step trajectory generated by the model and tail estimated by Q(sH). Assuming the dynamics model to be accurate up to the horizon, this yields higher accuracy in state-action values than the original estimate Q(s0).
On the other side, because of the fixed-length “rollouts” an into the future, potentially accumulating model errors or increasing value estimation error along the way. dynamics model to compute “rollouts” that are used to improve the targets for temporal difference learning.
Model-Based Policy Optimization (MBPO)
In MBPO [12], a dynamic transition distribution Tθ(st+1|st, at) parametrized by θ is learned via supervised learning on the sampled data from the data collection policy. During training, MBPO performs k-step rollouts using Tθ starting from state s ∈ Denv. MBPO iteratively collects samples from the environment and uses them to improve both the model and the policy further. Policy optimization algorithms may exploit these regions where the model is inaccurate.
Open Points
- How to use the model ensemble to encourage the policy to explore the state space where the different models disagree?
This article was written with the help of Jan Bieser and Moritz Zanger.
References
[1] V. Mnih, K. Kavukcuoglu, D. Silver, Al. Graves, I. Antonoglou, D. Wierstra, and M. Riedmiller, “Playing atari with deep reinforcement learning.”
[2] G. Dulac-Arnold, Daniel J. Mankowitz, and Todd Hester, “Challenges of real-world reinforcement learning.”
[3] T. Wang, X. Bao, I. Clavera, J. Hoang, Y. Wen E. Langlois, “Benchmarking Model-Based Reinforcement Learning”
[4] R. S. Sutton and A. Barto “ Reinforcement Learning: An Introduction”
[5] M. Deisenroth and C. Rasmussen, “PILCO: A Model-Based and DataEfficient Approach to Policy Search.”
[6] Y. Gal, and Z. Ghahramani, “Dropout as a Bayesian approximation: Representing model uncertainty in deep learning.”
[7] T. Kurutach, I. Clavera, Y. Duan, A. Tamar, and P. Abbeel, “Model-Ensemble Trust-Region Policy Optimization”
[8] I. Clavera, J. Rothfuss, J. Schulman, Y. Fujita, T. Asfour, and P. Abbeel, “Model-Based Reinforcement Learning via Meta-Policy Optimization,”
[9] J. Schulman, S.Levine, P. Abbeel, M. Jordan, P. Moritz, “Trust Region Policy Optimization”
[10] C. Finn, P. Abbeel, S. Levine, “Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks”
[11] V. Feinberg, A. Wan, I. Stoica, M. I. Jordan, J. E. Gonzalez, S. Levine, “Model-Based Value Estimation for Efficient Model-Free Reinforcement Learning”
[12] M. Janner, J. Fu, M. Zhang, and S. Levine, “When to trust your model: Model-based policy optimization.”
Uncertainty and Prediction in Model-based Reinforcement Learning was originally published in Becoming Human: Artificial Intelligence Magazine on Medium, where people are continuing the conversation by highlighting and responding to this story.
