First of all,
What is Euclidean Space and Non-Euclidean Space?

Euclidean Space
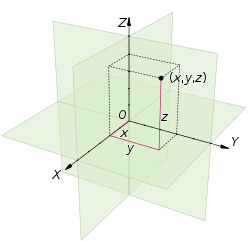
which involves the functional of 1 Dimensional, 2 Dimensional to N number of Dimension.
Whenever a Mathematician creates a formula in Geometry he has to prove that formula works for all Dimensional.

Let’s Get into non-euclidean Space.
Yeah, There is no Euclidean Space it’s about curve like hyperbolic and Sphere like space. Simply Euclidean looks for flat and Surface but non-Euclidean looks for curved.
This is much more useful than Euclidean space many times.
Neural networks are performing well in Euclidean Data. example: Text, Audio, Images, etc.
But what about Non-Euclidean Space? example: Graphs/Networks, Manifolds.Etc. (Likewise complex structures)
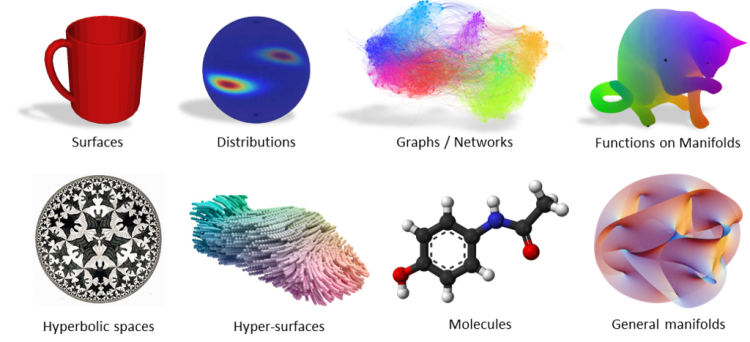
To know more about Non-Euclidean Space
So there comes Geometric Deep learning. Paper
Bronstein et al. first introduced the term Geometric Deep Learning (GDL) in their 2017 article “Geometric deep learning: going beyond euclidean data”
They are trying on the graphs and applying 3d model on CNN and etc.
Now we are going to look into one of that subdomain Graph lets jump into it.
Graphs
For a little bit, we will brush up on the basic stuff.
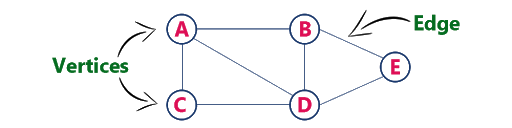
The graph is Simple G= (V, E)
Where, V= Vertices/Nodes. E =Edges.
Important types of Graph
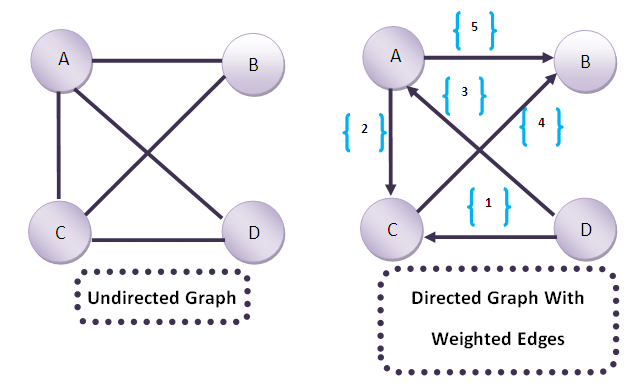
- Undirected Graph — have edges that do not have a direction
- Directed Graph — have edges with direction.
- Weighted Graph — edge has a numerical value called weight
the Weight/Labels can be numeric or string.
Nodes /vertices can have features , for example node A can be have features like it properties. (Weight and Features are not the same)
Computer Doesn’t understand the graph, So what to do? We can use Matrix
Trending AI Articles:

We know that any graph can be derived as the Matrix(N * M).
N-number of nodes
M-edges of graph
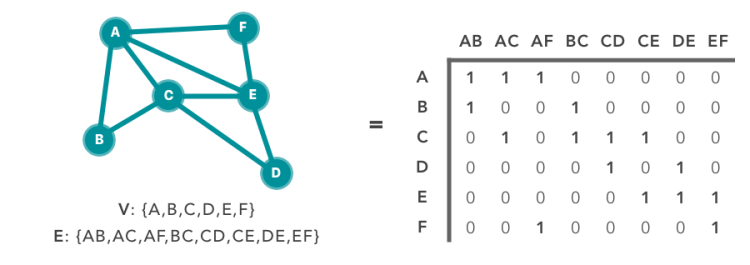
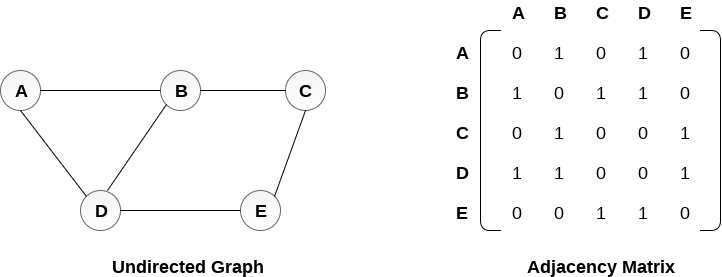
Adjacency matrix
Properties
- It is a Square matrix.
- Values can be either 0 or 1.
- Without self-loops, diagonals will be 0.
- It’s all about finding the Each node to another node adjacent or not. if not 0 else 1.
- Adjacency matrix can be done with a weighted graph, but there we will fill-up the weights instead of 0 and 1.
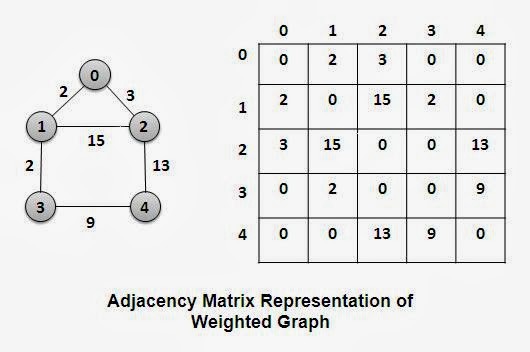
Simply , Collecting the neighborhood of the each node.
Degree Matrix
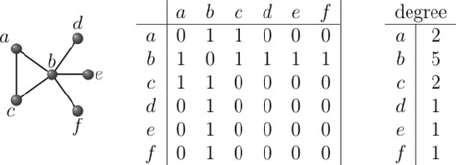
- It is a Diagonal matrix, just a count of how many edges are connected to the node (self-loop will be considered as 2).
Laplacian matrix
Laplacian = { D - A }
where ,
D - Degree Matrix
A - Adjacency Matrix
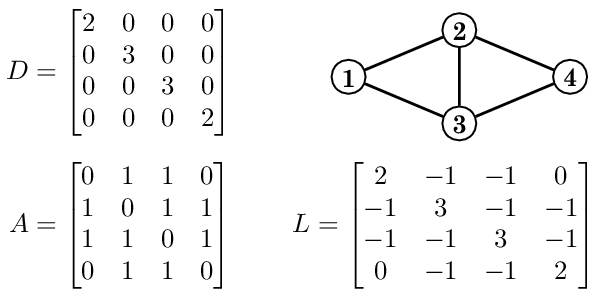
- It tells how smooth the graph is or the measurement of the smoothness of a vertex.
The architecture of Graph Neural Network
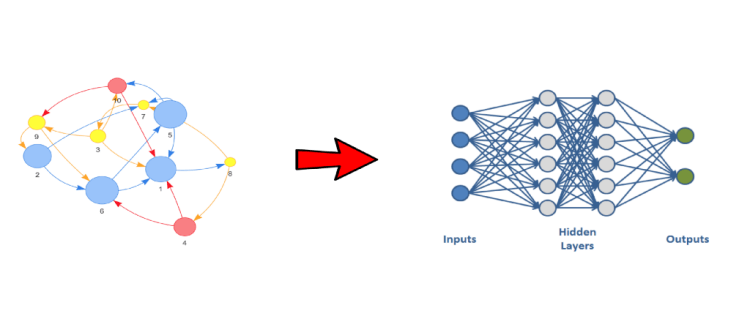
We know Neural networks and CNN are having fixed input values in the model But, Graphs are not fixed. So we have to do new approaches.
Get into CNN, CNN works in 3 steps
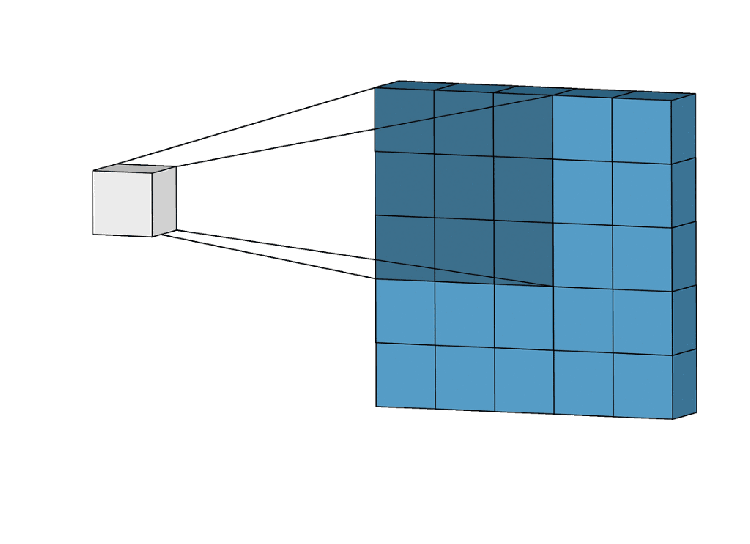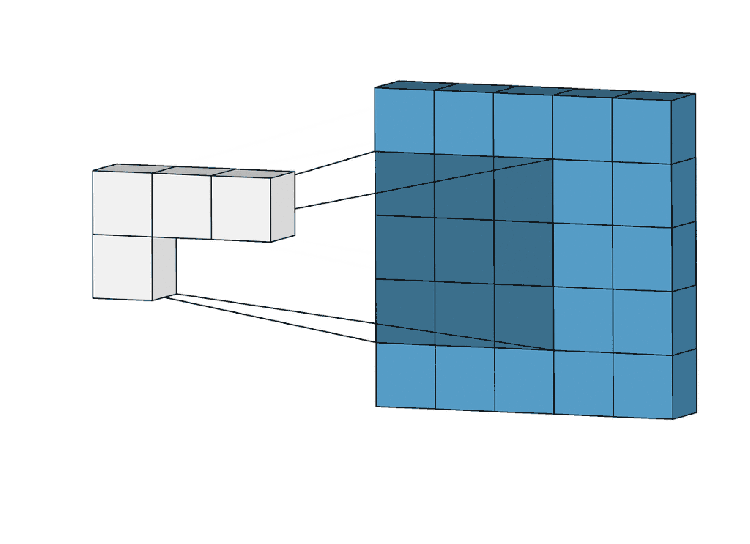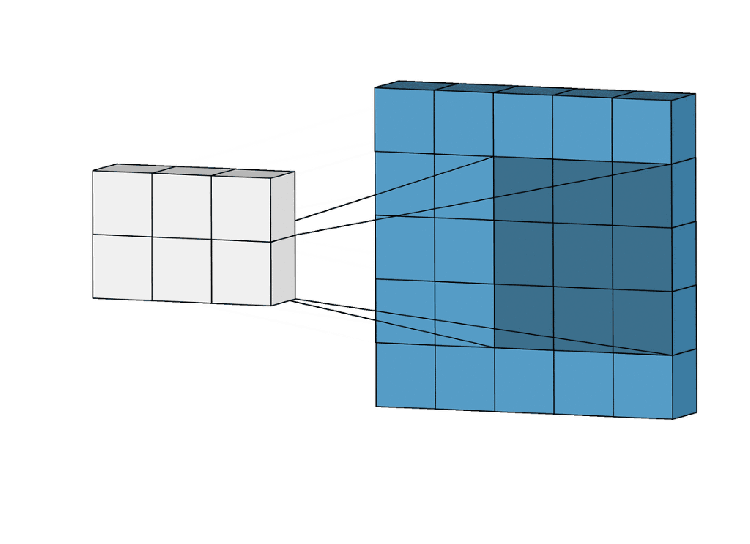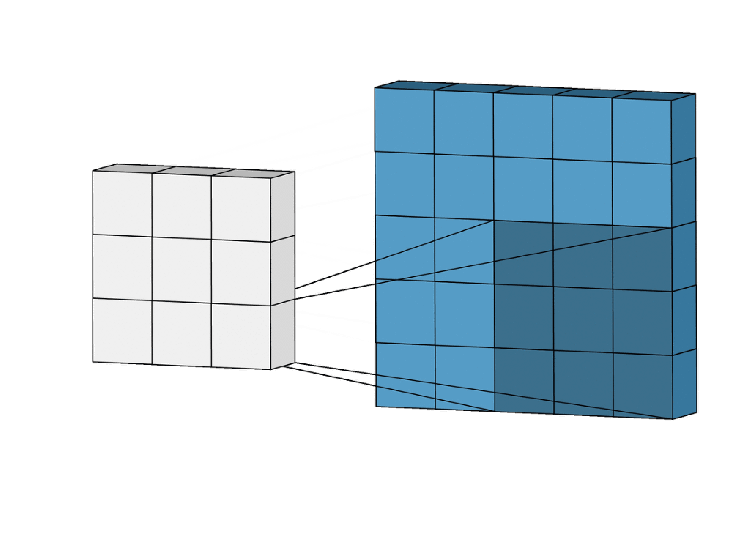
- Locality — Kernal /filter are taking a particular grid from beginning to end of the image, They are fixed grid.
- Aggregation — multiply with a mask by that particular grid and sum them up.
- Composition — Function of function (hidden layer computation f(f(x))…)
We can use the same methodology for GNN. In here locality will be considered for the neighborhood(how a node is connected to another node localizing the nodes), Aggregation means how they are contributing to their corresponding nodes by weights. Composition (stacking layers) passing to more layers.
Node Embedding
Aim : Similarity (u , v)= (z_u)^T(z_v) , z denotes the embedded space.
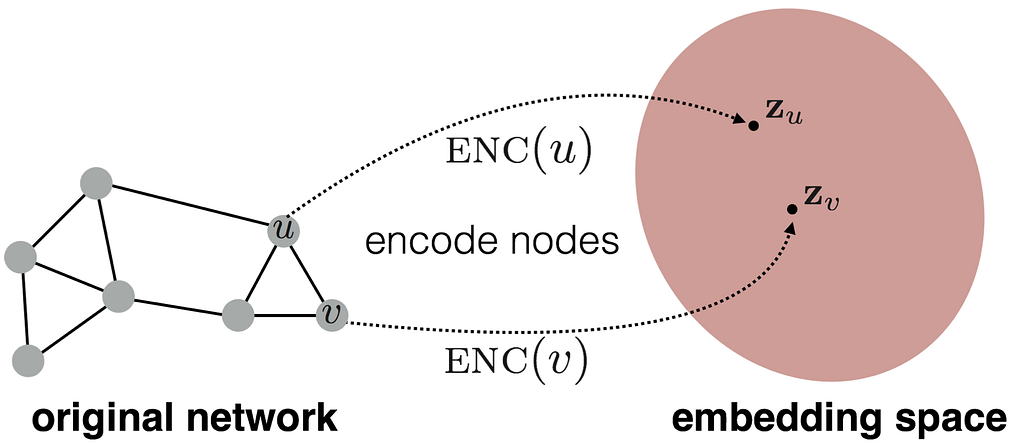
Node embedding converting the node into d-dimensional, where embedding space dimensional is less than the original network space.
encoding function ENC() converts the nodes into d-dimensional without changing the distance of u and v nodes.
Consider, u has the feature vector named x and v has y.
so , (z_u)(z_v) = (x)^T (y).
Locality (neighbors)
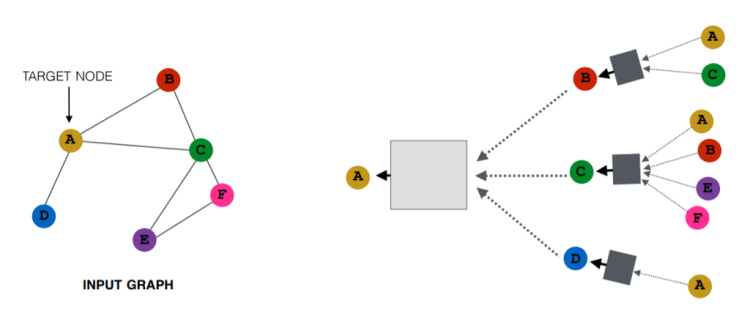
we have to create a computational graph for the target node.A’s neighborhood are B, C, D, so first B, C, D connected towards A, then connecting neighbors of neighbors, B is connected with A, C, Likewise, it goes
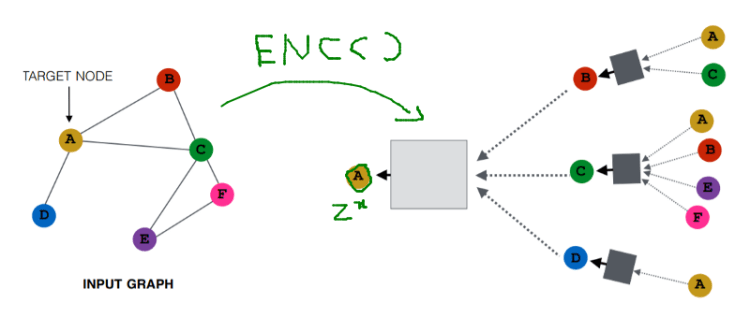
here it is working as an encoder function, A node to Z^x is actually an encoding. (Z^x is the feature vector of the A)
Also, all of the nodes have their own feature vector.
Aggregate (neighbors)
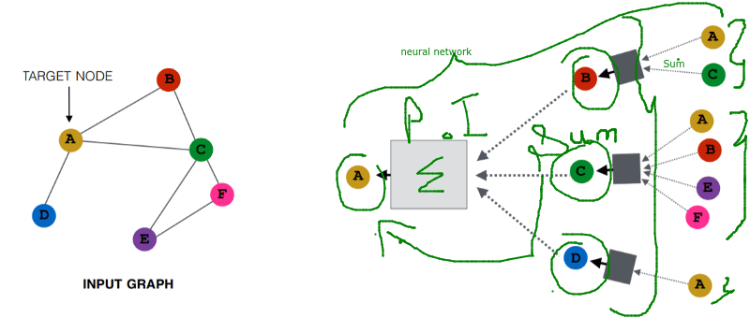
To get B we will sum up the A and C, likewise, for A we will sum up the B, C, D. It is a permutation invariant, that means (A+ B) and (B+A).
In the above, we have taken A has the target node, but after that, we have to take all the nodes as target node, for after this, b will be the target node that will give us the different Computational graph, like for other nodes also.
Forward propagation
We know how the Forward propagation works.
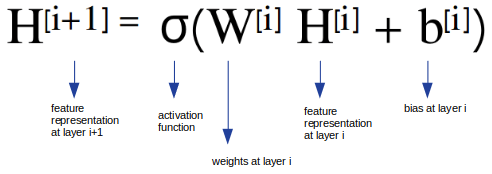
But how Graph Convolutional Networks works? there comes Spectral GCN. Spectral GCNs make use of the Eigen-decomposition of graph Laplacian matrix to implement this method of information propagation. GCN Paper
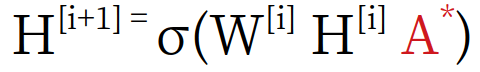
where A is the adjacency matrix. A* is the normalized value of A, For the Self-loops, we can multiply the A with an identity matrix.
Spectral Graph Convolution works as the message passing network by embedding the neighborhood node information along with it.
For training GCN we need 3 elements
- Adjacency matrix- learn the feature representations based on nodes connectivity.
- Node attributes- which are input features
- Edge attributes- data of Edge connectivity
Consider, X- as the input features, A as Adjacency matrix, D is degree matrix.
The dot product of Adjacency Matrix and Node Features Matrix represents the sum of neighboring node features
AX = np.dot(A,X)
Normalizing A is can be done in the way of

Doing the dot product with an inverse of degree matrix and AX but in this paper, Kipf and Welling are suggesting to do the symmetric normalization.

#Symmetrically-normalization
D_half_norm = fractional_matrix_power(D, -0.5)
DADX = D_half_norm.dot(A_hat).dot(D_half_norm).dot(X)
Otherwise, there is no need for Backpropagation. the function as it is just we are sending Adjacency matrix and input features with it, and only the forward propagation happens, each node is converted to the computational graph, and the forward propagation formula changes a little bit, also we are avoiding the bias b in the formula for simplicity sake, But the problem with the Graph neural network is data preparation, where we need an edge connectivity data and input features and adjacency matrix, the adjacency matrix is easy to create by one line of code, but the node, feature vectors and edge need to be clear.
For example, let us take Cora dataset :
The Cora dataset consists of 2708 scientific publications classified into one of seven classes. Each publication in the dataset is described by a 0/1-valued word vector indicating the absence/presence of the corresponding word from the dictionary. The dictionary consists of 1433 unique words.
- Nodes = Publications (Papers, Books …)
- Edges = Citations
- Node Features = word vectors
- 7 Labels = Publication type e.g. Neural_Networks, Rule_Learning, Reinforcement_Learning, Probabilistic_Methods…
Number of graphs: 1
Number of features: 1433
Number of classes: 7
Code for this Model building.
Don’t forget to give us your ? !




Geometric Deep learning with Graph Neural Network was originally published in Becoming Human: Artificial Intelligence Magazine on Medium, where people are continuing the conversation by highlighting and responding to this story.
