1. What is sigmoid function
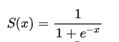
If you have worked on Logistic regression or Neural network problem you must have heard about Sigmoid function. It takes the input values between -∞ to ∞ and map them to values between 0 to 1. It is very handy when we are predicting the probability. For example, where email is spam or not, the tumor is malignant or benign. More detail about why to use sigmoid function in logistic regression is here
2. Why we calculate derivative of sigmoid function
We calculate the derivative of sigmoid to minimize loss function. Lets say we have one example with attributes x₁, x₂ and corresponding label is y. Our hypothesis is
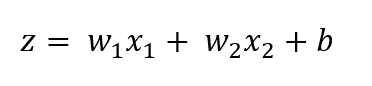
where w₁,w₂ are weights and b is bias.
Then we will put our hypothesis in sigmoid function to get the predict probability. i.e. values between 0 and 1.
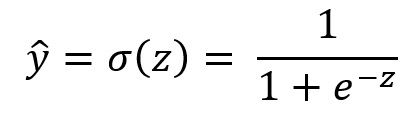
where y_hat is prediction probability of y being 1. And the loos function will be L(y_hat,y)
To minimize the loss function we need to do gradient descent, we will calculate the derivative of the loos function with respect to weights and bias and multiple that with learning rate alpha(α)and deduct that from our values of weights and bias. At the next we will use this new values of weights and bias. This iteration goes on until we hit global minima. Here is great article about gradient descent .
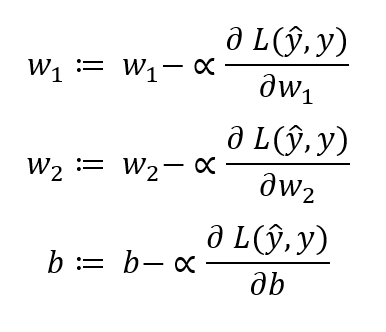
To calculate the derivative we have to back propagate. Because the loss function is depend upon sigmoid, sigmoid is depend upon hypothesis and hypothesis is depend on weight or bias.
w₁→z→ sigma(z) → L(y_hat, y)
By the chain rule of Derivative, derivative of loos function with respect to w₁
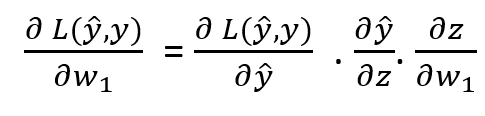
In this article we will talk about only middle term derivative of sigma function. Lets put value of y_hat

Now we will solve the derivative of sigmoid, We will treat this derivative as total derivative(not partial derivative) for more simplicity.
Trending AI Articles:
2. Generating neural speech synthesis voice acting using xVASynth
3. Derivation
Before going further I will recommend go through first seven Rules of Derivative from here.

Take the derivatives on both sides
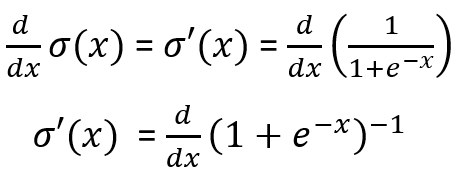
Applying power rule and chain rule

Again by the chain rule
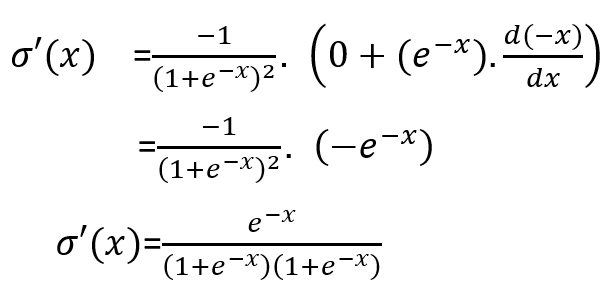
Add and subtract 1 in numerator
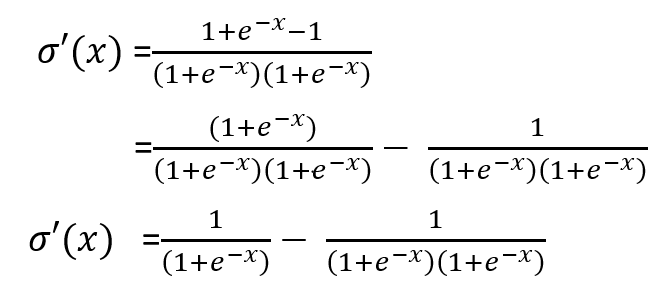
Lets take common multiple outside the bracket.

This is derivative of the sigma function
4.Plot
Lets take 50 numbers equality spaced between -10 to 10 and calculate sigmoid and derivatives of sigmoid for every number and plot it.
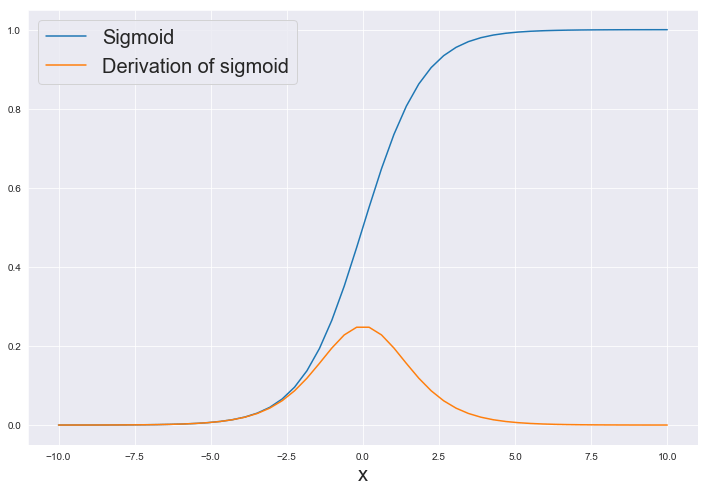
We know that Derivative is actually slope. Slope is defined as the ratio of change in Y to unite change in X.
We can see in plot at left where X= (-10), as we change X there is very less change in sigmoid(x), that’s why the slope or Derivative of sigmoid is nearly 0
But at the center of the plot, if change the X little bit, there is large change sigmoid(x), Moreover the slope is highest at X = 0,
As we go further right change of Y, to unit change of X is less so, again the slop is nearly zero.
These three conditions are depicted accurately by Derivative of sigmoid function (orange line) in the plot, Therefore we can say that our calculation good to go.
Thanks for reading. Feel free to refer below link’s for more details
5. References
Don’t forget to give us your ? !




What is Derivative of Sigmoid Function was originally published in Becoming Human: Artificial Intelligence Magazine on Medium, where people are continuing the conversation by highlighting and responding to this story.
